CENTRE OF GRAVITY

6.1 Centre of gravity:

The point at which whole weight of the body is assumed to be concentrated, is known as the centre of gravity of that body.

6.2 Centroid:

The point at which whole area of a plane(circle, rectangle, triangle, quadrilateral etc) is assumed to be concentrated is known as the centroid of that area.

It is represented by C.G or simply G.

•  The centroid and centre of gravity lie at the same point.

6.3 C.G of simple plane figures:

C.G of a uniform rod lies at it's middle point

C.G of a rectangle or a parallelogram lies at a point where it's both the diagonals meet. 

C.G of a triangle lies at a point at which the three medians of the triangle meet.

C.G of a circle lies at the centre of the circle.

6.4 Centroid of plane areas by Method of Moments:

Consider a plane area with a total area "A" whose C.G is to be determined. 

Let's divide this area into a number of smaller areas A₁ A₂ , A₃ ,  A₃....... etc

A =  A₁ + A₂ + A₃ + A₃ +............... 

Let OX &  OY be the reference axis. 

and,  X1= Distance of C.G of Area 1 from OY

X₂ = Distance of C.G of Area 2 from OY

X₃  = Distance of C.G of Area 3 from OY

X₄  = Distance of C.G of Area 4 from OY

and so on......... 

Moments of all the small areas    

 =   A1X1+A2X2+A3 X3  + A4 X4 +....... ______________(1)

Let "G"  be the C.G of the total area "A" located at a distance of X from the refrence axis OY

Then the moment of total area A about the axis OY = AX̅ __________(2)

The moments of all the small areas about axis OY must be equal to the moment of the total area A about OY. 

Hence equating equations (1) &  (2) we get, 

A1X1+ A2X2+ A3X3 + A4X4  +....... = AX̅

X̅  = (A1X1+ A2X2+ A3X3+ A4X4 +.....)/A

where,

         A = A1 + A2 + A3 + A4+ ........ 

Similarly, if we take the moments of all the small areas and the moment of total area A about the axis OX,  we get

Y̅ = (A1y1+A2y2+A3y3+A4y4+.....)/A

Y̅ = Distance of G from the axis OX. 

y1  = Distance of C.G of Area1 from the refrence axis OX. 

y₂ = Distance of C.G of Area2 from the refrence axis OX. 

y₃  = Distance of C.G of Area3 from the refrence axis OX. 

y₄  = Distance of C.G of Area4 from the refrence axis OX. 

and so on......... 

NOTE:

• The axis about which moments are taken is known as axis of refrence.

• Axis of refrence for plane figures is generally taken as the lowest line of the figure for determining y and the left line of the figure for determining X.

• If the section is symmetrical about any of the axis, then the C.G will lie on the axis of symmetry.

6.5 CENTRE OF GRAVITY OF COMPOSITE SECTIONS:


L- SECTION:
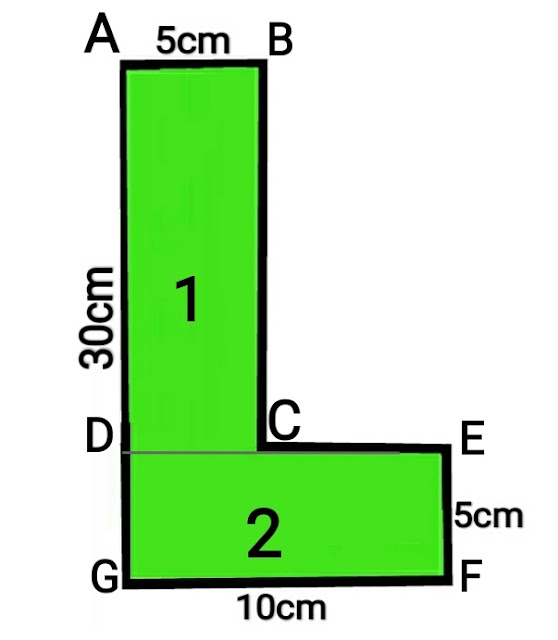
Example 6.5.1: Find the C.G of the given L-SECTION. 

Solution:


The given L-SECTION is divided into two rectangular areas, ABCD & DEFG

Since L-section is not symmetrical about any axis, hence there will be two reference axis. The lowest line GF will be taken as reference axis for calculating y and the left line AG will be taken as reference axis for calculating X.

Y̅ = Distance of C.G from reference line GF

A1 = Area of rectangle ABCD=25×5=125cm²

y1= Distance of C.G of rectangle ABCD from reference line GF = 5+25/2 = 17.5cm

A₂ = Area of rectangle DEFG = 10×5 = 50cm²

y₂ = Distance of C.G of rectangle DEFG from reference line GF = 5/2 = 2.5cm

= (125×17.5 + 50×2.5)/(125+50)

Y̅ = 13.214cm Ans

X̅ = Distance of C.G from reference line AG

X1 = Distance of C.G of rectangle ABCD from refrence line AG = 5/2 = 2.5 cm

X₂ = Distance of C.G of rectangle DEFG from refrence line AG = 10/2 = 5cm

= (125×2.5 + 50×5)/(125+50)

X̅ =3.214cm Ans

Hence C.G of the given

L-section lies at a distance of 13.214cm from GF and 3.214cm from AG.

T- SECTION: 
Example 6.5.2: Find the C.G of the given T-SECTION.

Solution:


The given T-section is divided into two rectangular areas ABCD & EFGH.

Since the T-section is symmetrical about y-axis, so the centre of gravity will lie on y-axis. 

Let's take the bottom line GF as reference axis for calculating Y̅.

Y̅ = Distance of C.G of T-section from the bottom line GF(axis of reference)

A1 = Area of rectangle ABCD = 12×3= 36cm²

y1 = Distance of C.G of A1 from the reference line GF =10+3/2=11.5cm

A2 Y̅=8.545cm = Area of rectangle EFGH = 10×3= 30cm²

y₂ = Distance of C.G of A₂ from the reference line GF =10/2=5cm

[(36×11.5)+(30×5)]÷[36+30]

=8.545cm

Y̅=8.545cm Ans

Hence C.G of the given T-section lies at a distance of 8.545cm from the reference axis GF

I- SECTION: 

Example 6.5.3: Find the C.G of the given I-SECTION. 

Solution:

The given I-section is divided into three rectangular areas ABCD, EFGH &  IJKL

Since the I section is symmetrical about y-axis, so the centre of gravity of the given I section will lie on the y-axis. 

Let's take the bottom line KJ as the reference axis. 

Y̅ = Distance of C.G of I-section from the bottom line KJ (axis of reference) 

A1 = Area of rectangle ABCD 

=20×10=200cm²

y1 = Distance of C.G of rectangle ABCD from refrence line KJ

=20+10+10/2=35cm

A₂=Area of rectangle EFGH

=20×10=200cm²

y₂= Distance of C.G of rectangle EFGH from refrence line KJ

= 10+20/2= 20cm

Similarly, y₃= Distance of C.G of rectangle IJKL (A₃) from reference line KJ = 10/2=5cm

A₃ = 20×10= 200cm²

[(200×35)+(200×20)+(200×5)]÷(200+200+200)

= 20cm

Y̅ = 20cm Ans